Daten analysieren
Die Fähigkeit, Daten zu analysieren, ist in unserer zunehmend datengetriebenen Welt von entscheidender Bedeutung. Datenanalysen ermöglichen es uns, Zusammenhänge zu verstehen, Risiken einzuschätzen und begründete Entscheidungen zu treffen.
Info für Lehrende
Mehr zu SchuBu+
Wahrscheinlichkeiten verstehen
Die Interpretation von Wahrscheinlichkeiten ermöglicht es uns, fundierte Entscheidungen zu treffen. Die Wettervorhersage ist ein klassisches Beispiel dafür, wie Wahrscheinlichkeiten genutzt werden, um uns auf zukünftige Ereignisse vorzubereiten.

Die Meteorologinnen und Meteorologen sagen voraus, dass es morgen eine Regenwahrscheinlichkeit von
Es bedeutet, ...
Wie funktionieren Wahrscheinlichkeiten?
Wahrscheinlichkeiten sind mathematische Maße, die uns sagen, wie sicher (100 %) oder unsicher (0 %) ein Ereignis ist.
Zum Beispiel: Die Zeit läuft zu
Wenn ein Ereignis die Wahrscheinlichkeit von einem anderen Ereignis nicht beeinflusst, sind die Ereignisse unabhängig.
Zum Beispiel: Die morgige Regenwahrscheinlichkeit ist unabhängig davon, ob du gestern dein Essen aufgegessen hast.
Schätze die Wahrscheinlichkeit folgender Aussagen, indem du den Regler verschiebst!
Statistisch denken
Statistiken sammeln und organisieren Daten. Damit ermöglichen sie es, Muster und Beziehungen zu identifizieren und daraus Schlussfolgerungen zu ziehen.
Würfle 20-mal mit einem Würfel oder erfinde 20 Würfelergebnisse! Du hast 10 Minuten Zeit, diesen Vorgang zu wiederholen. Danach beantworte die Klassenfrage:
Medien und Statistiken
Medien neigen dazu, mehr über dramatische Ereignisse zu berichten. Vor allem, wenn diese selten sind. Das heißt, es wird vor allem über Ereignisse berichtet, bei denen die Wahrscheinlichkeit gering ist, dass sie auch im Leben der Zuseherinnen und Zuseher eintreten. Das hat meist zur Folge, dass Menschen diese Ereignisse als häufiger oder bedrohlicher einschätzen, als es die statistischen Daten tatsächlich nahelegen.

Es ist daher empfehlenswert, Statistiken kritisch zu hinterfragen und den Kontext zu verstehen. Das bedeutet, dass Zahlen und Fakten stets in einem größeren Zusammenhang betrachtet werden sollten.
Absolute Zahlen (3 Flugzeugabstürze) allein können einen eingeschränkten Blickwinkel bieten, während relative Zahlen (3 von 50 Millionen Flügen = 0,00000006 %) eine tiefergehende Perspektive aufzeigen können.
Relative Zahlen können den Kontext verschleiern (50 % haben beim Test die Note 1), wenn die absolute Anzahl (2 Personen haben beim Test teilgenommen) nicht berücksichtigt wird.

Korrelation und Kausalität
In der Statistik ist es wichtig, stets zwischen Korrelation (Zusammenhang) und Kausalität (Ursache-Wirkung) zu unterscheiden. Nur weil zwei Dinge miteinander verbunden sind, bedeutet das nicht unbedingt, dass eines das andere verursacht.
Scheinkorrelation aufdecken
Seht euch jeweils die beiden Beispiele und die dazugehörige Behauptung an! Kann das stimmen? Besprecht gemeinsam in der Klasse!
Info für Lehrende„Die Abnahme der Anzahl an brütenden Storchenpaaren hat einen Geburtenrückgang in Österreich zur Folge.“
„Verzehrt man ab Beginn einer Erkältung Schokolade, ist man nach zwei Wochen wieder gesund.“
Um Scheinkorrelationen aufzudecken, gilt es herauszufinden, ob der Zusammenhang auf Zufall beruht oder ob eine echte Ursache dahintersteckt. Bevor man auf eine Kausalität schließt, sollte man vorher alternative Erklärungen in Betracht ziehen!
Studien lesen
Es gibt viele Faktoren, die Wissenschaftlerinnen und Wissenschaftler bei der Erstellung und Durchführung einer Studie beachten müssen. Liest man einen Bericht über eine Studie, hilft es folgende 3 Faktoren im Auge zu behalten:
Eine Studie sollte- eine aussagekräftige Anzahl an Menschen einbeziehen (repräsentative Stichprobe),
- über einen längeren Zeitraum durchgeführt werden (Langzeitstudie),
- und andere Einflussfaktoren berücksichtigen oder ausschließen können (Kontrollgruppen).
Medien und Studien
Medien spielen eine entscheidende Rolle bei der Verbreitung wissenschaftlicher Erkenntnisse. Gleichzeitig besteht die Herausforderung, die Glaubwürdigkeit und die richtige Interpretation dieser Informationen sicherzustellen.
Lies die Zusammenfassung der Studie und bewerte die dazugehörigen Schlagzeilen!
Eine Studie, durchgeführt von Bildungsforschern an einer führenden Universität, untersuchte den Zusammenhang zwischen der Menge der Hausaufgaben und der schulischen Leistung bei Grundschulkindern. Über 1000 Schülerinnen und Schüler wurden über einen Zeitraum von einem Jahr beobachtet und ihre Noten sowie ihre Hausaufgabenmengen wurden dokumentiert. Die Ergebnisse deuten darauf hin, dass eine moderate Menge an Hausaufgaben positiv mit der schulischen Leistung korreliert, während übermäßige Hausaufgaben eine negative Auswirkung haben können.
Auch in der Werbung werden Studienergebnisse oft genutzt, um Produkte positiv darzustellen. Häufig werden dabei Fakten verzerrt, was die Konsumenten dazu verleiten kann, falsche Schlussfolgerungen zu ziehen.
Klicke dich durch die Slides und entlarve den Marketingtrick!
Diagramme vergleichen
Daten können auf unterschiedlichste Arten visualisiert werden. Die Wahl der Darstellung sollte allerdings gut gewählt sein, da sie Auswirkungen auf die Wahrnehmung und Interpretation der Daten haben kann.
Welche Darstellung ist gut gewählt?
Die Klasse 3b hat an einer Umfrage teilgenommen. Das Ergebnis soll als Diagramm in der Schulzeitung veröffentlicht werden. Nun wird diskutiert, welche der drei Darstellungen genommen werden soll.
Wähle aus, welches Diagramm das Ergebnis am besten wiedergibt!
Ergebnis der Umfrage „Welches Tierbaby findest du am niedlichsten?"

- Hundewelpen scheinen dominierend
- Andere Ergebnisse wirken vernachlässigbar und irrelevant
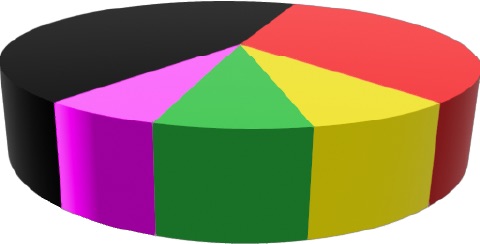
- Unbeliebtere Tierbabys scheinen bedeutender
- Hundewelpen haben zwar viele Stimmen, die anderen Tiere haben jedoch auffälligere Mehrheit
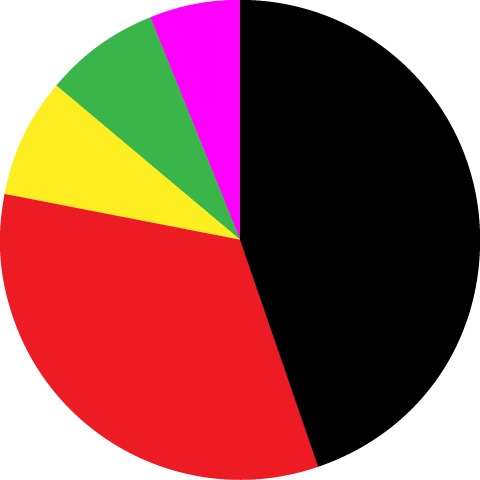
- Kreisdiagramm gibt Ergebnis am besten wieder
- Keine perspektivische Verzerrung (Achtung: Auch Farbwahl kann die Wahrnehmung beeinflussen!)
Manipulation statistischer Darstellungen
Je weniger Bildschirmzeit, desto mehr Taschengeld – das ist die Regel. Leider hat sich deine Bildschirmzeit zum Vorjahr verdoppelt. Du willst deine Eltern nicht anlügen, aber auch nicht weniger Taschengeld. Die Auswertung kannst du nicht mehr ändern. Dafür kannst du die statistische Darstellung nach belieben auswählen.
Bearbeite das diesjährige Diagramm so, dass es scheinbar keine auffällige Veränderung zum Vorjahr aufweist!
Besprecht anschließend in Kleingruppen, welche Methoden ihr verwendet habt!
Hacks und Tricks
Datenwissenschaft einfach erklärt
- Statistik hilft uns, Daten zu sammeln.
Beispiel: Mithilfe von Statistik könnten wir zählen, wie viele Menschen in einer Stadt Fahrrad fahren, und das in einem Diagramm zeigen. - Studien beantworten Fragen durch Forschung.
Beispiel: Um herauszufinden, ob mehr Radwege zu mehr Radfahrern führen, machen wir eine Studie. Wir befragen oder beobachten Menschen, um zu sehen, wie oft sie Fahrrad fahren und warum. - Wahrscheinlichkeit sagt uns, wie wahrscheinlich oder sicher die Ergebnisse sind.
Beispiel: Um sicherzugehen, dass dieser Zusammenhang (Anzahl Radfahrer und Anzahl Radwege) nicht zufällig ist, nutzen wir Wahrscheinlichkeit. Sie zeigt uns, wie sicher oder unsicher das Ergebnis ist.



